Modélisation du Moteur Brushless

Nous vous proposons de modéliser ensemble le moteur brushless (BLDC).

Un moteur brushless est une machine électrique de la catégorie des machines synchrones, dont le rotor est constitué d’un ou de plusieurs aimants permanents et peut être pourvu d’un capteur de position rotorique (capteur à effet Hall, synchro-résolver, codeur incrémental…).

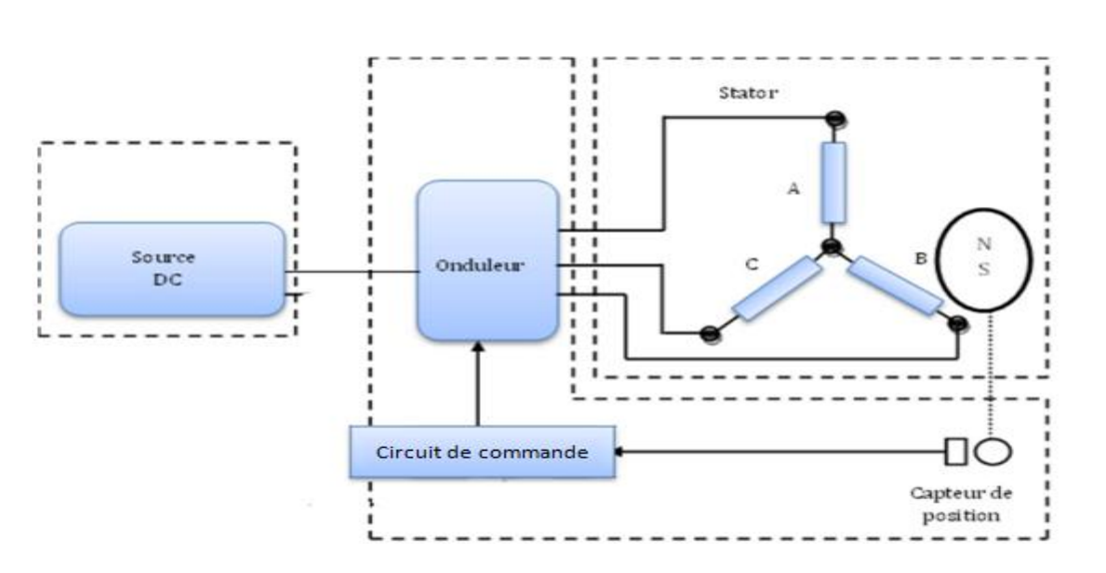
Schéma de commande d’un moteur Brushless

Les équations électriques

Les équations électriques qui régissent le fonctionnement d’un moteur BLDC sont données par les équations suivantes :

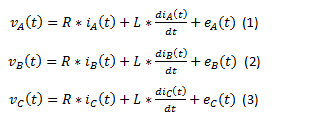
Vue que le système est équilibré:

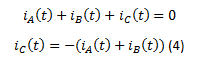
(4) dans (3) donne:

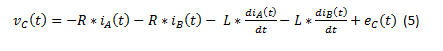
(1), (2) et (5) impliquent:

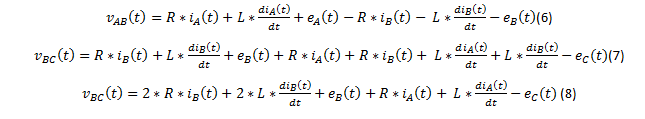
(8) implique:

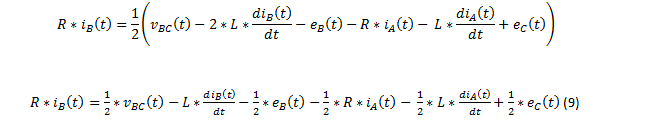
(9) dans (6) donne:

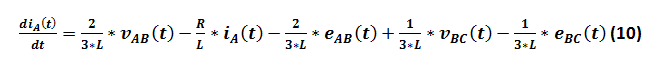
(10) dans (8) donne:

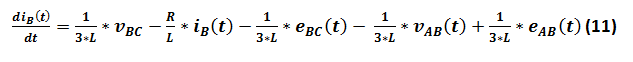
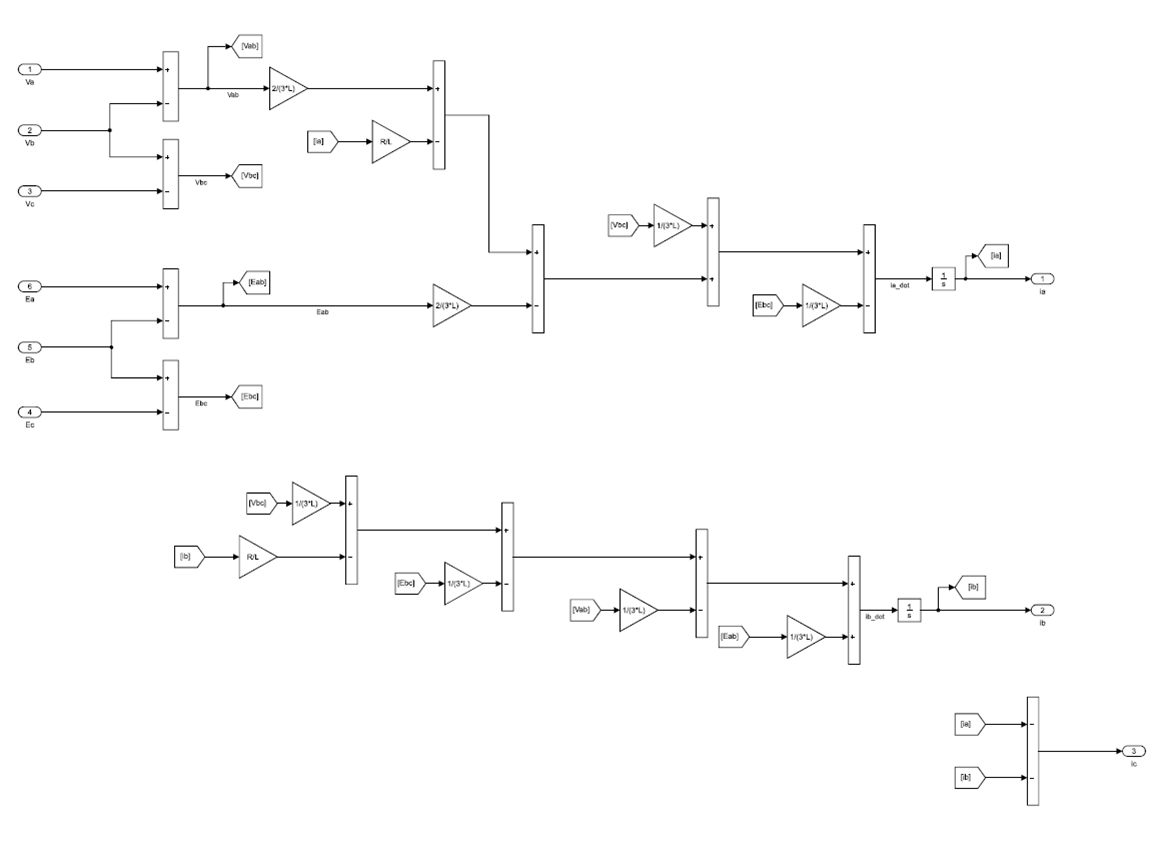
Équations électriques

Le couple électrique

Le couple électrique généré par un moteur BLDC se calcul comme suit :

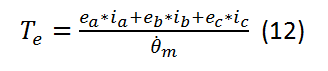
Avec et la force contre électromotrice et le courant sur chaque phase et  la vitesse de rotation du rotor.

Les expressions des sont définies comme suit :

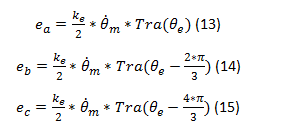
où est la constante de force contre électromotrice et l’angle électrique qui se calcul comme suit avec  le nombre de pair de pôle.

est une fonction d’onde trapézoïdal définit comme suit :

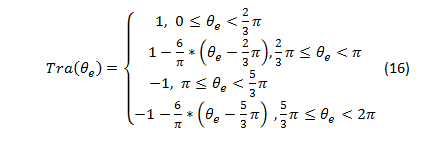
13, 14 et 15 dans 12 donne:

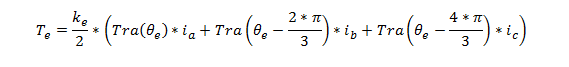
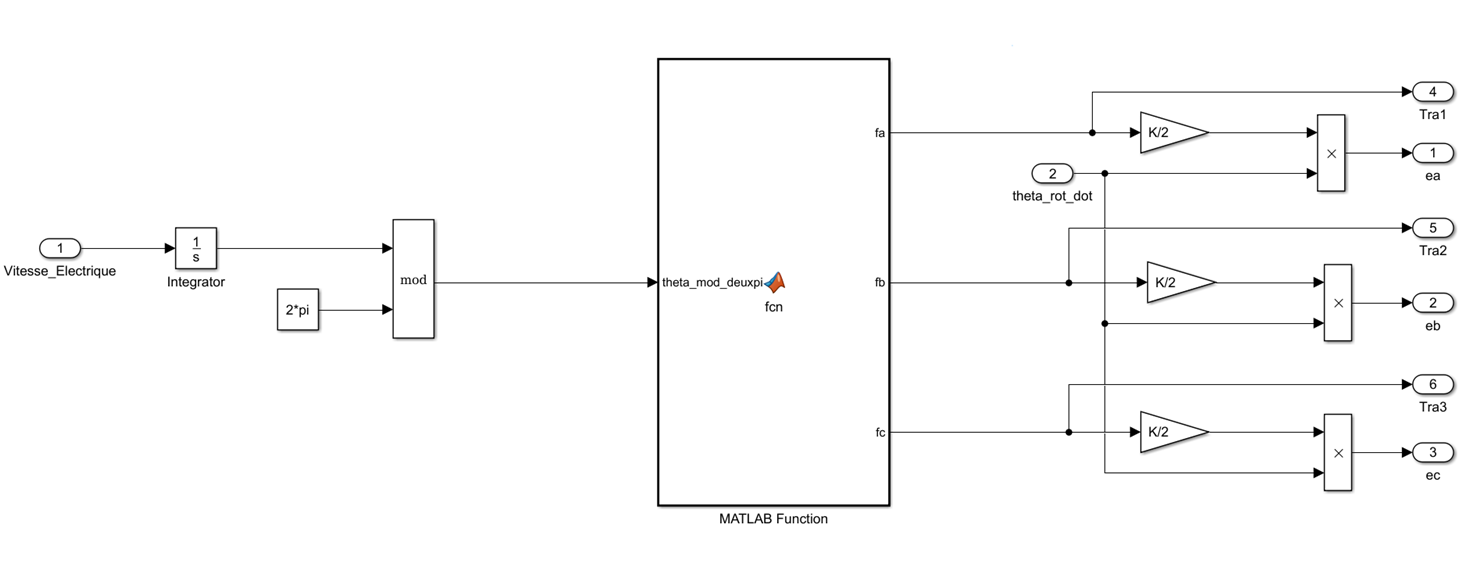
function [fa,fb,fc]= fcn(theta_mod_deuxpi)
fa=0;
fb=0;
fc=0;
if (theta_mod_deuxpi>= 0)&& (theta_mod_deuxpi<= pi/3)
    fa=1;
    fb=-1;
    fc=1-(6/pi)*theta_mod_deuxpi;
elseif (theta_mod_deuxpi> pi/3)&& (theta_mod_deuxpi<= (2*pi/3))
     fa=1;
     fb=(6/pi)*theta_mod_deuxpi-3;
     fc=-1;
elseif (theta_mod_deuxpi>(2*pi/3))&& (theta_mod_deuxpi<=pi)
     fa=5-(6/pi)*theta_mod_deuxpi;
     fb=1;
     fc=-1;
elseif (theta_mod_deuxpi>pi)&&(theta_mod_deuxpi<=(4*pi/3))
     fa=-1;
     fb=1;
     fc=(6/pi)*theta_mod_deuxpi -7;
elseif (theta_mod_deuxpi>(4*pi/3))&&(theta_mod_deuxpi<=(5*pi/3))
    fa=-1;
    fb=9-(6/pi)*theta_mod_deuxpi;
    fc=1;
elseif (theta_mod_deuxpi>(5*pi/3))&&(theta_mod_deuxpi<=2*pi)
    fa=(6/pi)*theta_mod_deuxpi-11;
    fb=-1;
    fc=1;
end
end

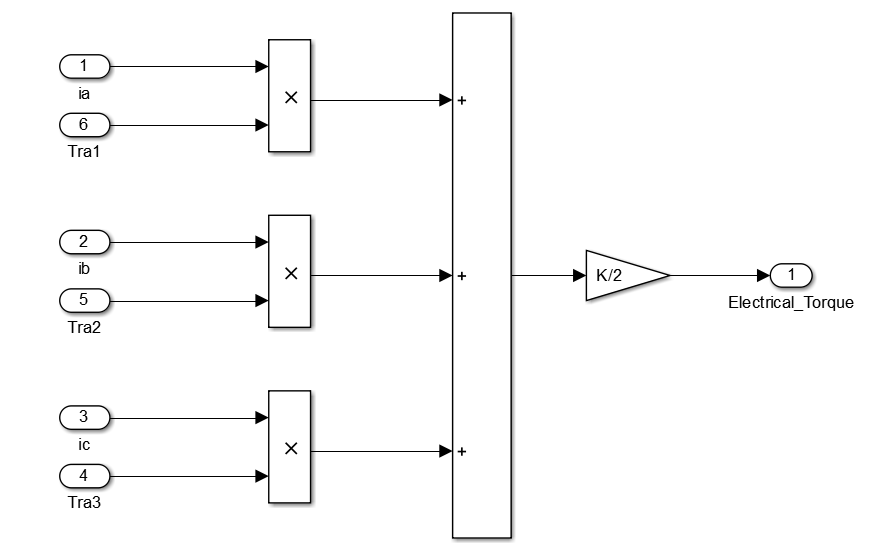
Coupe électrique

Équations mécaniques

L’équation mécanique qui régit le fonctionnement d’un moteur BLDC est la suivante :

Où est le couple électrique, B est le coefficient de frottement visqueux J  l’inertie du rotor,  est le couple de charge,  et  respectivement la vitesse et l’accélération du rotor.

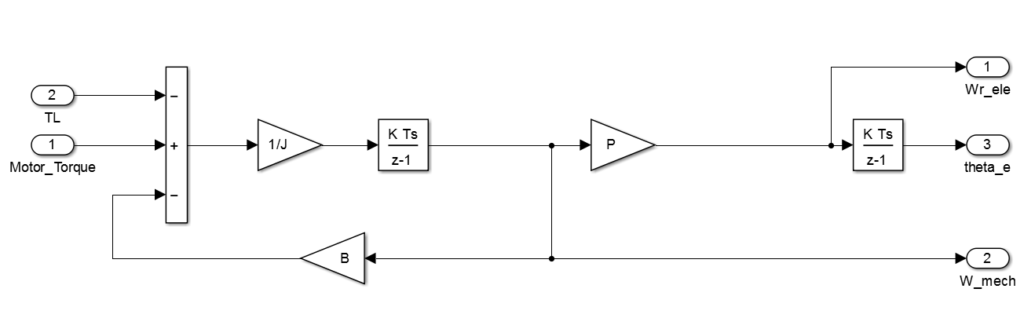
Équations mécaniques

Capteur effet Hall

Sur une évolution de la position angulaire du rotor entre 0 et 2*pi nous avons les capteurs effet hall qui évolues selon le tableau suivant :

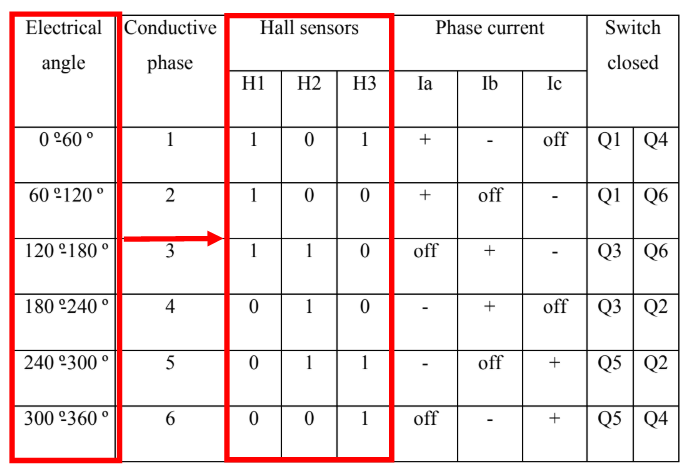
function [Ha,Hb,Hc]= fcn(theta_mod_deuxpi)
Ha=0;
Hb=0;
Hc=0;
if (theta_mod_deuxpi>= 0)&& (theta_mod_deuxpi<= pi/3)%entre 0°-60°
    Ha=1;
    Hb=0;
    Hc=1;
elseif (theta_mod_deuxpi> pi/3)&& (theta_mod_deuxpi<= (2*pi/3))%entre 60°-120°
    Ha=1;
    Hb=0;
    Hc=0;
elseif (theta_mod_deuxpi>(2*pi/3))&& (theta_mod_deuxpi<=pi)%entre 120°-180°
    Ha=1;
    Hb=1;
    Hc=0;
elseif (theta_mod_deuxpi>pi)&&(theta_mod_deuxpi<=(4*pi/3))%entre 180°-240°
    Ha=0;
    Hb=1;
    Hc=0;
elseif (theta_mod_deuxpi>(4*pi/3))&&(theta_mod_deuxpi<=(5*pi/3))%entre 240°-300°
    Ha=0;
    Hb=1;
    Hc=1;
elseif (theta_mod_deuxpi>(5*pi/3))&&(theta_mod_deuxpi<=2*pi)%entre 300°-360°
    Ha=0;
    Hb=0;
    Hc=1;
end
end

Séquence de commutation des transistors

Lorsque les pôles du rotor passent à côté des capteurs effet hall, ces derniers donne 1 ou 0, pour indiquer que le pôle nord où sud est en train de passer à coté des capteurs. En se basant sur cette logique de commutation des capteurs effets hall, nous avons la séquence de commutation des transistors selon tableau suivant.

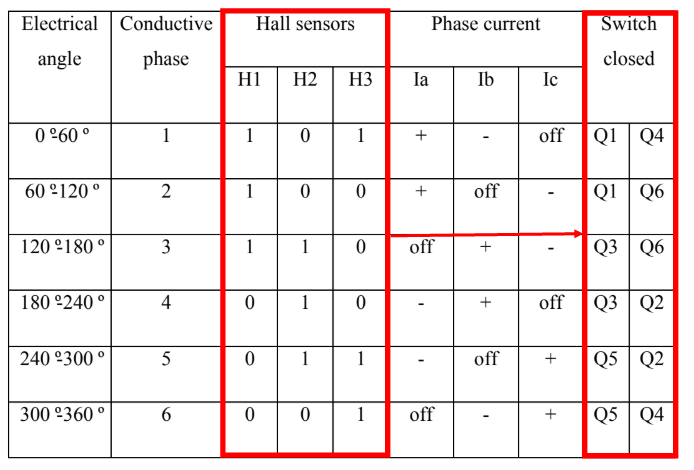
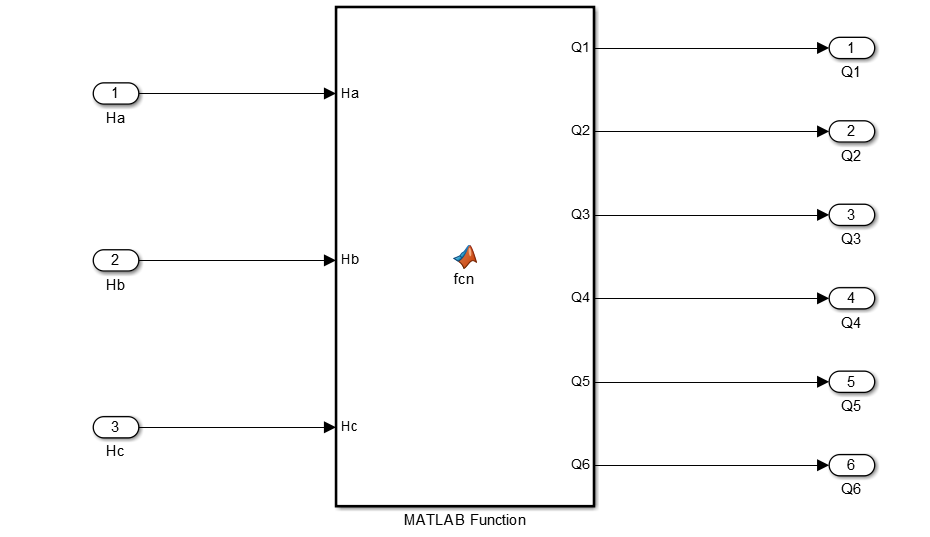
function [Q1,Q2,Q3,Q4,Q5,Q6]= fcn(Ha,Hb,Hc)
Q1=0;
Q2=0;
Q3=0;
Q4=0;
Q5=0;
Q6=0;
if (Ha==1)&& (Hb==0)&&(Hc==1)
    Q1=1;
    Q2=0;
    Q3=0;
    Q4=1;
    Q5=0;
    Q6=0;  
elseif (Ha==1)&& (Hb==0)&&(Hc==0)
    Q1=1;
    Q2=0;
    Q3=0;
    Q4=0;
    Q5=0;
    Q6=1;
elseif (Ha==1)&& (Hb==1)&&(Hc==0)
    Q1=0;
    Q2=0;
    Q3=1;
    Q4=0;
    Q5=0;
    Q6=1;
elseif (Ha==0)&& (Hb==1)&&(Hc==0)
    Q1=0;
    Q2=1;
    Q3=1;
    Q4=0;
    Q5=0;
    Q6=0;
elseif (Ha==0)&& (Hb==1)&&(Hc==1)
    Q1=0;
    Q2=1;
    Q3=0;
    Q4=0;
    Q5=1;
    Q6=0;
elseif (Ha==0)&& (Hb==0)&&(Hc==1)
    Q1=0;
    Q2=0;
    Q3=0;
    Q4=1;
    Q5=1;
    Q6=0;
end
end

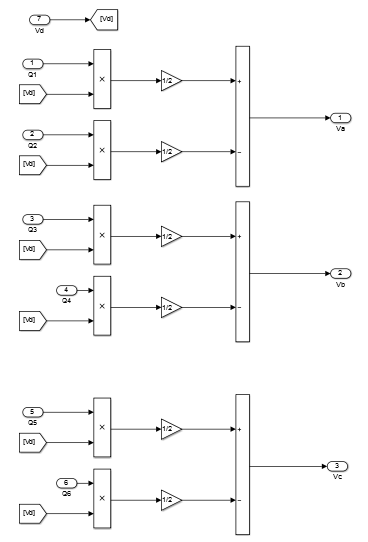
Calcul des tensions à appliquer au moteur BLDC

Selon le circuit de la figure ci-dessous les tensions triphasées se calcul avec les formules suivantes :

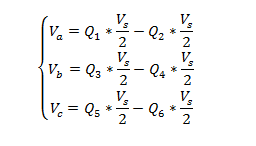
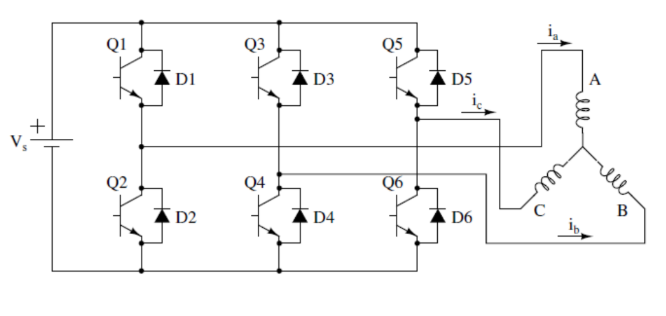
Schéma drive BLDC