Interférence de deux ondes sinusoïdales sous MATLAB
On se propose de construire une interface graphique, qui affiche l’interférence de deux ondes sinusoïdales de même amplitude. La vitesse angulaire de la première onde est fixe et égale à 1, et avec une phase réglée à zéro.
Les données de la première onde étant considérées comme invariables, l’utilisateur peut définir la phase de la seconde onde et établir le rapport de sa vitesse angulaire en fonction de la première onde.
On cherche à montrer les effets des modifications de vitesse angulaire et de phase de la deuxième composante sur la forme de l’onde résultante.
Pour cela l’interface devra contenir :
- Une figure principale;
- Deux axes pour les représentations graphiques;
- Deux boutons pour le rafraichissement et la remise à zéro des courbes;
- Quatre zone de texte statique;
- Deux zones de textes éditable.
Dans la figure ci dessous, vous avez une illustration du résultat attendu:
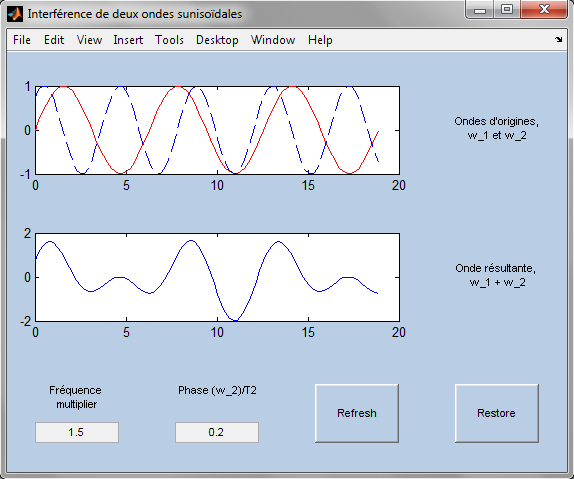
Interférence de deux ondes sinusoïdales
Le bouton « Restore » permet de remettre à zéro les courbes et le bouton « Refresh » permet de rafraichir la représentation graphique de l’onde résultante.
Solution
Nous avons fait le choix, de coder cette interface graphique sous la forme d’un programme, qui va se comporter comme un trieur. Pour cela, nous allons structurer le programme avec un Switch qui aura 4 états:
- mpt_init : initialise l’interface utilisateur graphique
- mpt_omega : définit la vitesse angulaire de la deuxième onde
- mpt_phase : définit la phase de la deuxième onde
- mpt_rafraichir : trace la superposition des deux ondes
Le programme prend en entrée une variable, nommée flag. Le Switch évalue la valeur du flag qui lui est donnée et aiguille le programme vers le cas correspondant.
function MPT_Interference(flag) % netoyage clc; % initialise sans argument if nargin < 1 flag = 'mpt_init'; end
Lorsque l’on exécute le programme sans paramètres, la fonction MATLAB nargin, détecte un nombre d’arguments inférieur à 1 et affects la chaine de caractère « mpt_init » à la variable flag.
Initialisation de linterface
Dans le cas d’une demande d’initialisation, la variable flag = ‘mpt_init‘.
switch flag case 'mpt_init' % suppression de la figure appelante s'il existe if ~isempty(gcf) delete(gcf); end % couleur de la figure colorfigure = [185/255 205/255 229/255]; % Définition de la première onde % omega1 : vitesse angulaire de la 1ere onde, rad/s % T : période de la 1ere onde, s % t : échelle de temps, s omega1 = 1; T = 2*pi / omega1; t = 0:T/30:3*T; w1 = sin(omega1*t); % rapport entre la deuxième onde sur la première multipl = 1; % rapport de phase par rapport à la période de la deuxième onde phase = 0;
On regarde d’abord si la figure existe déjà. Si c’est le cas, on la supprime. Ensuite on définit les données invariables de la première onde.
Le code suivant permet de créer et d’affecte à la figure, un nom et une couleur de fond.
% création de la figure principale H_fig = figure( 'NumberTitle', 'off', ... 'Name', 'Interférence de deux ondes sunisoïdales', ... 'Color', colorfigure);
Création des zones de textes
Ensuite, on crée deux zones d’édition et un label pour chaque zone d’édition. Ces zones d’édition permettront à l’utilisateur de modifier la valeur de la vitesse angulaire ainsi que la valeur de la phase de la deuxième onde
% création de la zone de text "Multiplicateur de fréquence" uicontrol(H_fig,'Units', 'normalized', ... 'Position', [0.05 0.07 0.15 0.05], ... 'Style', 'Edit', ... 'String', num2str(multipl), ... 'Tag', 'omega', ... 'CallBack', ('MPT_Interference(''mpt_omega'')')); % Création du label uicontrol(H_fig,'Units', 'normalized', ... 'Position', [0.05 0.13 0.15 0.08], ... 'Style', 'Text', ... 'BackGround', colorfigure, ... 'String', 'Multiplicateur de fréquence'); % Création de la zone de text "Phase w_2/T2" uicontrol(H_fig,'Units', 'normalized', ... 'Position', [0.3 0.07 0.15 0.05], ... 'Style', 'Edit', ... 'String', num2str(phase), ... 'Tag', 'rapport_phase', ... 'CallBack', ('MPT_Interference(''mpt_phase'')')); % Création du label uicontrol(H_fig,'Units', 'normalized', ... 'Position', [0.3 0.13 0.15 0.08], ... 'Style', 'Text', ... 'BackGround', colorfigure, ... 'String', 'Phase w_2/T2');
La propriété CallBack, permet de définir la fonction, qui sera appelée lorsqu’on modifie la valeur de la zone d’édition. En l’occurrence, c’est le programme principal MPT_Interference(), qui sera appelé avec l’argument »mpt_omega » ou « mpt_phase ».
La propriété position permet de définir la position de l’objet graphique dans la figure principale. On l’utilise comme suite : ‘position’, [gauche, bas, largeur, Hauteur].
- gauche et bas : définissent les coordonnées x, y de l’objet, en partant du coin bas à gauche de la figure principale.
La propriété Units, nous permet d’exprimer les dimensions en unité normalisée. C’est à dire en pourcentage de la taille de la figure principale.
Création des boutons
Création des deux boutons, pour rafraichir et pour réinitialiser l’application.
% Création du bouton "Refresh" uicontrol(H_fig,'Units', 'normalized', ... 'Position', [0.55 0.07 0.15 0.14], ... 'Style', 'Pushbutton', ... 'String', 'Refresh', ... 'BackGround', colorfigure, ... 'CallBack', ('MPT_Interference(''mpt_rafraichir'')')); % Création du bouton "Restore" uicontrol(H_fig,'Units', 'normalized', ... 'Position', [0.8 0.07 0.15 0.14], ... 'Style', 'Pushbutton', ... 'String', 'Restore', ... 'BackGround', colorfigure, ... 'CallBack', ('MPT_Interference(''mpt_init'')'));
Création des axes
Le code suivant permet de créer les deux axes, avec pour chacun une zone de texte pour servir de description.
% Création de la legende des ondes d'origines uicontrol(H_fig,'Units', 'normalized', ... 'Position', [0.8 0.71 0.15 0.14], ... 'Style', 'Text', ... 'BackGround', colorfigure, ... 'String', 'Ondes d''origines, w_1 et w_2'); % Création de la legende de l'onde résultant uicontrol(H_fig,'Units', 'normalized', ... 'Position', [0.8 0.36 0.15 0.14], ... 'Style', 'Text', ... 'BackGround', colorfigure, ... 'String', 'Onde résultante, w_1 + w_2'); % Création des axes Ha_up = axes('Position', [0.05 0.71 0.65 0.21]); plot (t, w1, 'r-'); Ha_down = axes('Position', [0.05 0.36 0.65 0.21]); plot (t, w1, 'r-'); xlabel('Time, S')
Gestion des données dans l’IHM
On utilise un tableau de cellules pour stocker les données transmises entres les différents segments de l’interface. Ensuite on enregistre le tableau de cellules résultant Mydata dans la propriété UserData associée à la figure, un dispositif qui permet de transmettre des données entre les différentes parties d’une fonction récursives.
% allocation d'espace mémoire Mydata = cell (7); Mydata{1} = omega1; Mydata{2} = t; Mydata{3} = w1; Mydata{4} = multipl; Mydata{5} = phase; Mydata{6} = Ha_up; Mydata{7} = Ha_down; % Enregistrement sur la mémoire de l'interface set (gcf, 'UserData', Mydata);
Définition de la vitesse angulaire de la deuxième onde
Dans le cas où flag = ‘mpt_omega’, c’est-à-dire lorsque, l’utilisateur change la valeur de la vitesse angulaire de la deuxième onde sur la première.
Ce bout de code va récupérer la nouvelle valeur rentrée par l’utilisateur.
case 'mpt_omega' % lecture de la valeur de omega h_omega = findobj (gcf, 'Tag', 'omega'); multipl = str2double (get(h_omega, 'String'));
Ensuite, on récupère les données contenues dans le tableau Mydata, puis on crée la deuxième onde.
% lecture des donnees contenu sur l'interface Mydata = get (gcf, 'UserData'); omega1 = Mydata{1}; t = Mydata{2}; w1 = Mydata{3}; Ha_up = Mydata{6}; % représenter la 2eme courbe omega2 = omega1 * multipl; w2 = sin (omega2*t);
Enfin, on trace la deuxième onde sur le premier axe et on met à jour le tableau de données Mydata.
% affichage de la courbe de w2 axes (Ha_up); plot (t, w1, 'r-', t, w2, 'b--'); % sauvegarde de la nouvelle valeur de multipl Mydata{4} = multipl; set(gcf, 'UserData', Mydata);
Définition de la phase de la deuxième onde
Dans le cas où flag = ‘mpt_phase’, c’est-à-dire lorsque, l’utilisateur change la valeur de la phase de la deuxième onde.
Ce bout de code va récupérer la nouvelle valeur rentrée par l’utilisateur:
case 'mpt_phase' % Lecture de la valeur phase h_phase = findobj (gcf, 'Tag', 'rapport_phase'); phase = str2double (get(h_phase, 'String'));
Ensuite, on récupère les données contenues dans le tableau de cellules Mydata, puis on crée la deuxième onde:
% lecture des données de l'interface Mydata = get (gcf, 'UserData'); omega1 = Mydata{1}; t = Mydata{2}; w1 = Mydata{3}; multipl = Mydata{4}; Ha_up = Mydata{6}; % representer la 2eme courbe omega2 = omega1 * multipl; T2 = 2*pi/omega2; delta = phase*T2; w2 = sin(omega2*t + delta);
On trace la deuxième onde sur le premier axe et on met à jour le tableau de données Mydata:
% représentation de la 1ere courbe axes (Ha_up); plot (t, w1, 'r-', t, w2, 'b--'); % sauvegarde de la nouvelle valeur de phase Mydata{5} = phase; set(gcf, 'UserData', Mydata);
Tracer de la superposition des deux ondes
Dans le cas où flag = ‘mpt_rafraichir’, c’est-à-dire lorsque l’utilisateur clique sur le bouton Rafraichir, on trace alors l’onde résultante sur la deuxième axe :
case 'mpt_rafraichir' % lecture des données de l'interface Mydata = get (gcf, 'UserData'); omega1 = Mydata{1}; t = Mydata{2}; w1 = Mydata{3}; multipl = Mydata{4}; phase = Mydata{5}; Ha_down = Mydata{7}; % représentation de la courbe résultante omega2 = omega1 * multipl; T2 = 2*pi/omega2; delta = phase*T2; w2 = sin(omega2*t + delta); w = w1 + w2; axes (Ha_down); plot (t, w, 'b-'); end



Comments