Modélisation du Moteur Brushless
Nous vous proposons de modéliser ensemble le moteur brushless (BLDC).
Un moteur brushless est une machine électrique de la catégorie des machines synchrones, dont le rotor est constitué d’un ou de plusieurs aimants permanents et peut être pourvu d’un capteur de position rotorique (capteur à effet Hall, synchro-résolver, codeur incrémental…).
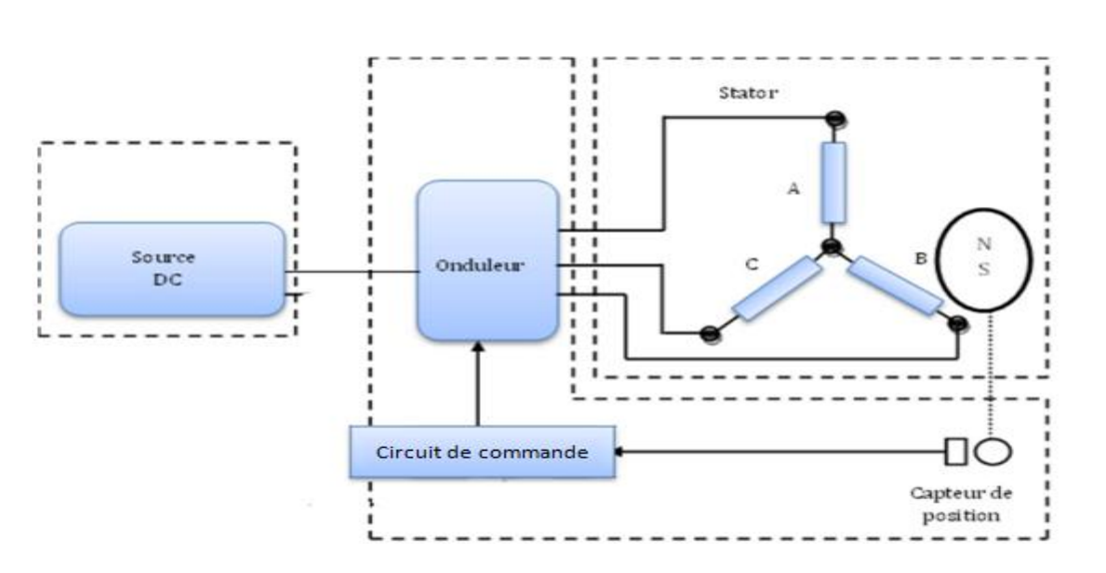
Schéma de commande d’un moteur Brushless
Les équations électriques
Les équations électriques qui régissent le fonctionnement d’un moteur BLDC sont données par les équations suivantes :
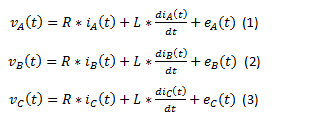
Vue que le système est équilibré:
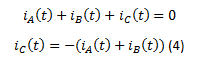
(4) dans (3) donne:
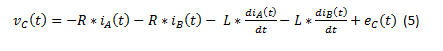
(1), (2) et (5) impliquent:
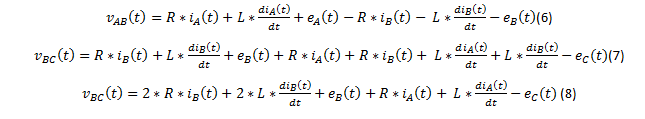
(8) implique:
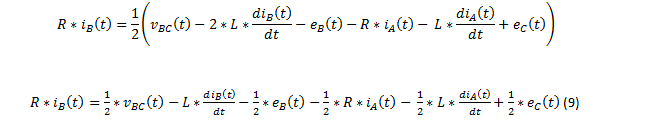
(9) dans (6) donne:
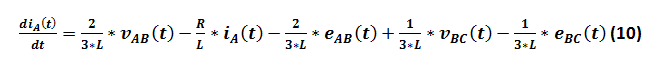
(10) dans (8) donne:
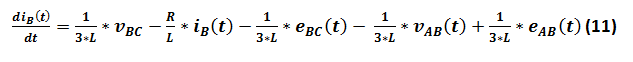
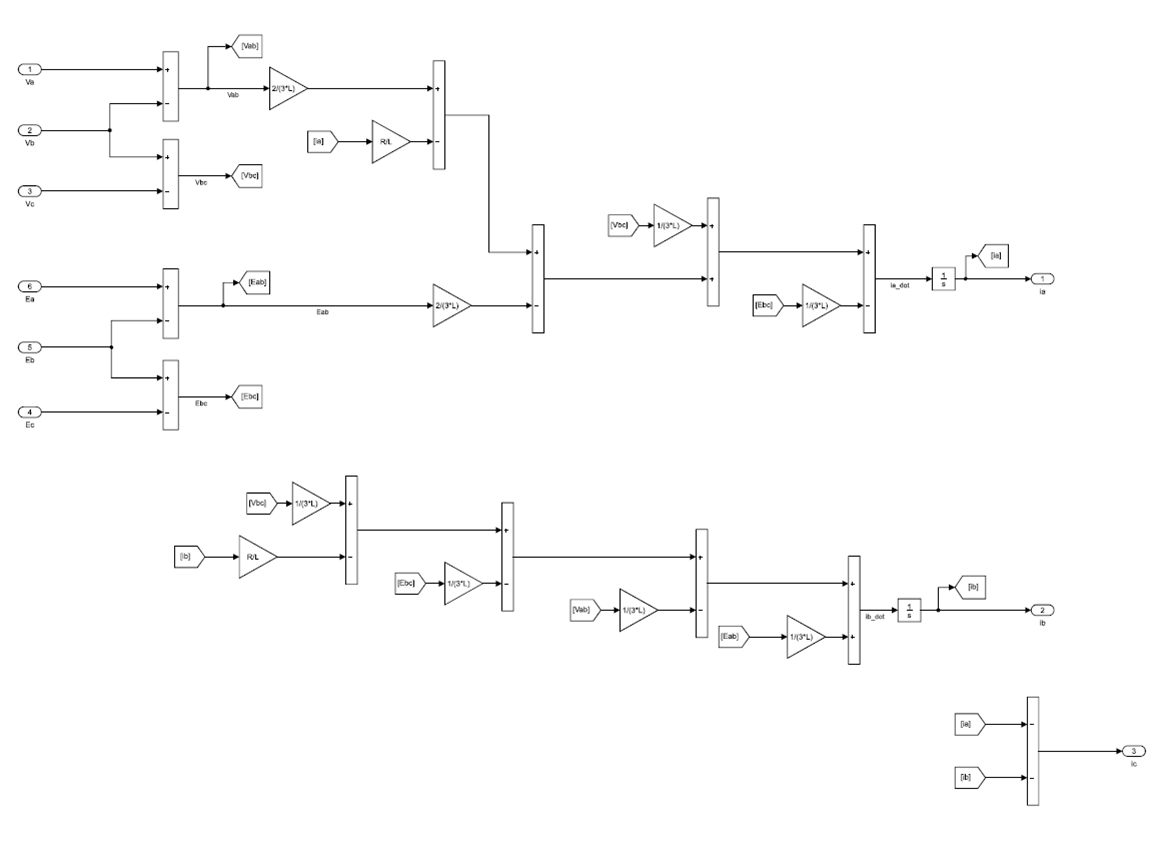
Équations électriques
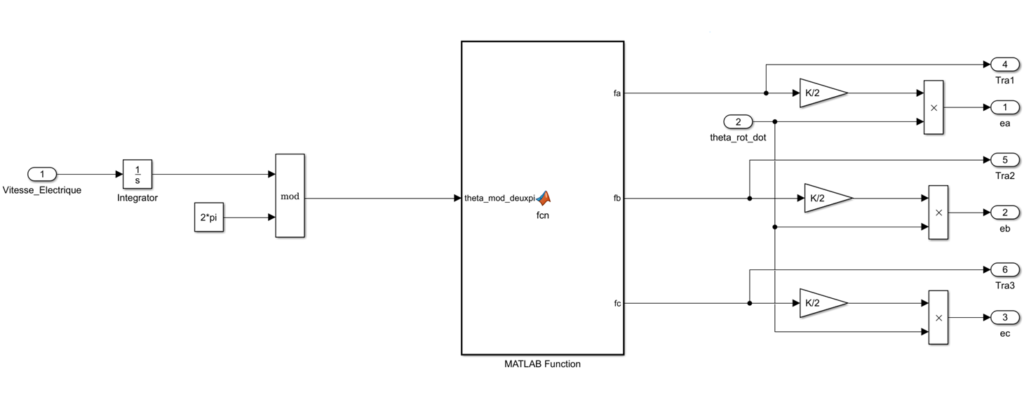
Le couple électrique
Le couple électrique généré par un moteur BLDC se calcul comme suit :
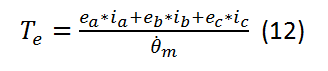
Avec![]() et
et ![]() la force contre électromotrice et le courant sur chaque phase et
la force contre électromotrice et le courant sur chaque phase et ![]() la vitesse de rotation du rotor.
la vitesse de rotation du rotor.
Les expressions des ![]() sont définies comme suit :
sont définies comme suit :
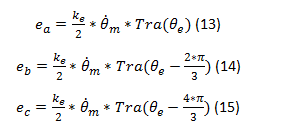
où ![]() est la constante de force contre électromotrice et
est la constante de force contre électromotrice et ![]() l’angle électrique qui se calcul comme suit
l’angle électrique qui se calcul comme suit ![]() avec le nombre de pair de pôle.
avec le nombre de pair de pôle.
![]() est une fonction d’onde trapézoïdal définit comme suit :
est une fonction d’onde trapézoïdal définit comme suit :
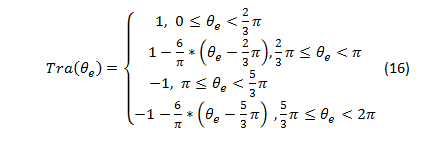
13, 14 et 15 dans 12 donne:
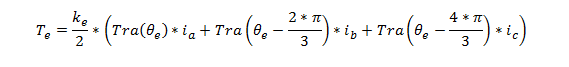
function [fa,fb,fc]= fcn(theta_mod_deuxpi) fa=0; fb=0; fc=0; if (theta_mod_deuxpi>= 0)&& (theta_mod_deuxpi<= pi/3) fa=1; fb=-1; fc=1-(6/pi)*theta_mod_deuxpi; elseif (theta_mod_deuxpi> pi/3)&& (theta_mod_deuxpi<= (2*pi/3)) fa=1; fb=(6/pi)*theta_mod_deuxpi-3; fc=-1; elseif (theta_mod_deuxpi>(2*pi/3))&& (theta_mod_deuxpi<=pi) fa=5-(6/pi)*theta_mod_deuxpi; fb=1; fc=-1; elseif (theta_mod_deuxpi>pi)&&(theta_mod_deuxpi<=(4*pi/3)) fa=-1; fb=1; fc=(6/pi)*theta_mod_deuxpi -7; elseif (theta_mod_deuxpi>(4*pi/3))&&(theta_mod_deuxpi<=(5*pi/3)) fa=-1; fb=9-(6/pi)*theta_mod_deuxpi; fc=1; elseif (theta_mod_deuxpi>(5*pi/3))&&(theta_mod_deuxpi<=2*pi) fa=(6/pi)*theta_mod_deuxpi-11; fb=-1; fc=1; end end
Coupe électrique
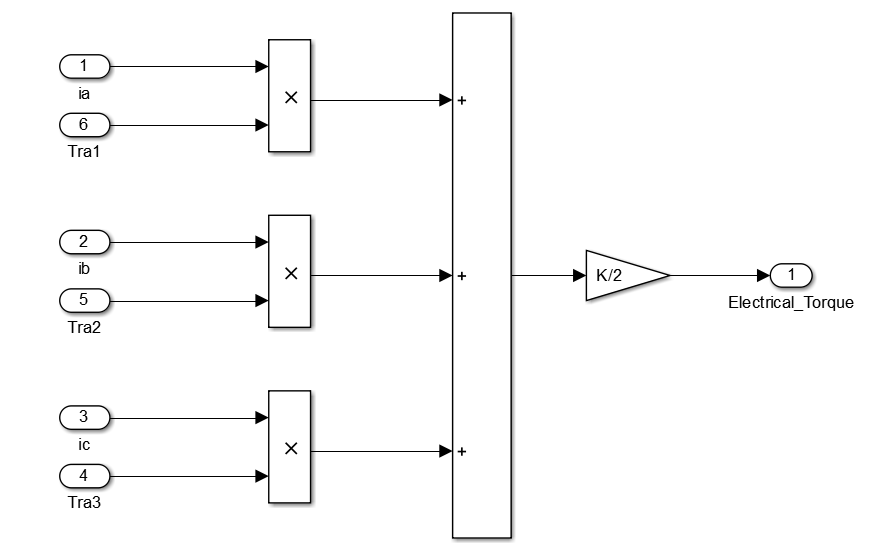
Équations mécaniques
L’équation mécanique qui régit le fonctionnement d’un moteur BLDC est la suivante :
![]()
Où ![]() est le couple électrique, B est le coefficient de frottement visqueux J l’inertie du rotor,
est le couple électrique, B est le coefficient de frottement visqueux J l’inertie du rotor, ![]() est le couple de charge,
est le couple de charge, ![]() et
et ![]() respectivement la vitesse et l’accélération du rotor.
respectivement la vitesse et l’accélération du rotor.
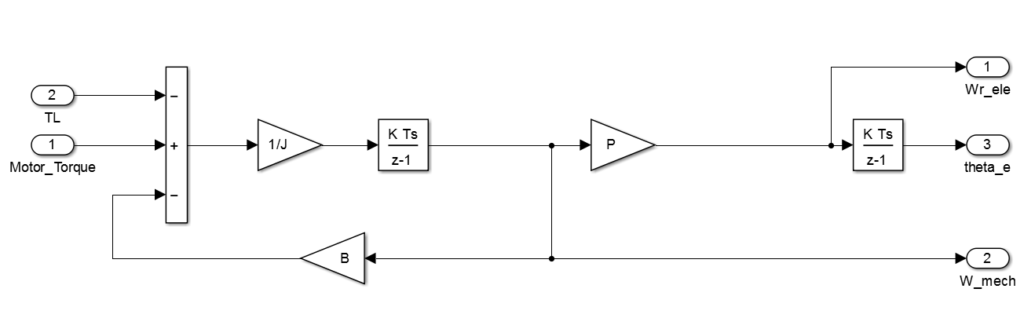
Équations mécaniques
Capteur effet Hall
Sur une évolution de la position angulaire du rotor entre 0 et 2*pi nous avons les capteurs effet hall qui évolues selon le tableau suivant :
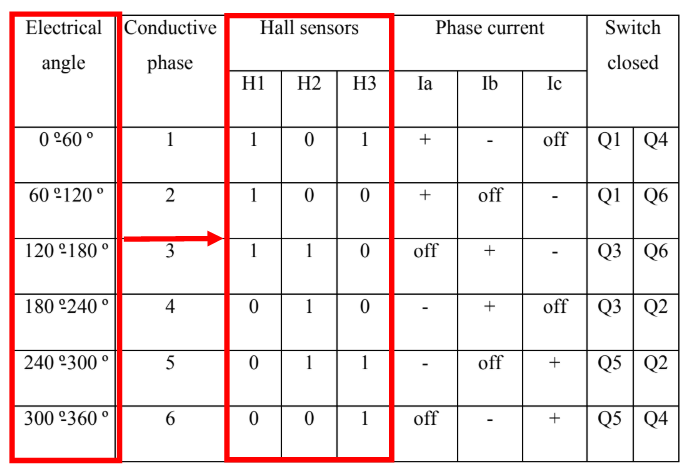
function [Ha,Hb,Hc]= fcn(theta_mod_deuxpi) Ha=0; Hb=0; Hc=0; if (theta_mod_deuxpi>= 0)&& (theta_mod_deuxpi<= pi/3)%entre 0°-60° Ha=1; Hb=0; Hc=1; elseif (theta_mod_deuxpi> pi/3)&& (theta_mod_deuxpi<= (2*pi/3))%entre 60°-120° Ha=1; Hb=0; Hc=0; elseif (theta_mod_deuxpi>(2*pi/3))&& (theta_mod_deuxpi<=pi)%entre 120°-180° Ha=1; Hb=1; Hc=0; elseif (theta_mod_deuxpi>pi)&&(theta_mod_deuxpi<=(4*pi/3))%entre 180°-240° Ha=0; Hb=1; Hc=0; elseif (theta_mod_deuxpi>(4*pi/3))&&(theta_mod_deuxpi<=(5*pi/3))%entre 240°-300° Ha=0; Hb=1; Hc=1; elseif (theta_mod_deuxpi>(5*pi/3))&&(theta_mod_deuxpi<=2*pi)%entre 300°-360° Ha=0; Hb=0; Hc=1; end end
Séquence de commutation des transistors
Lorsque les pôles du rotor passent à côté des capteurs effet hall, ces derniers donne 1 ou 0, pour indiquer que le pôle nord où sud est en train de passer à coté des capteurs. En se basant sur cette logique de commutation des capteurs effets hall, nous avons la séquence de commutation des transistors selon tableau suivant.
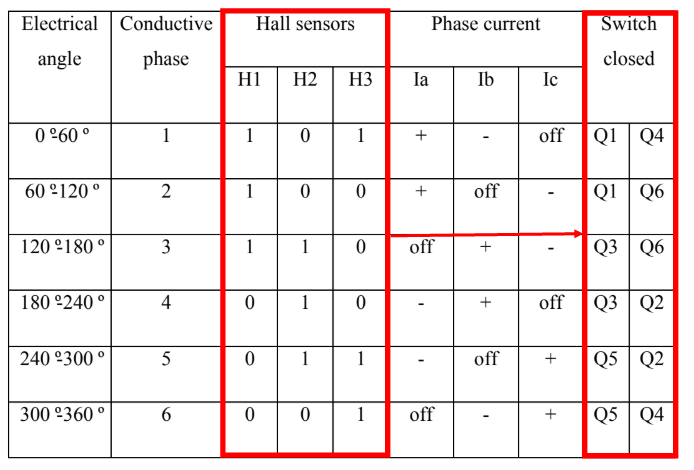
function [Q1,Q2,Q3,Q4,Q5,Q6]= fcn(Ha,Hb,Hc) Q1=0; Q2=0; Q3=0; Q4=0; Q5=0; Q6=0; if (Ha==1)&& (Hb==0)&&(Hc==1) Q1=1; Q2=0; Q3=0; Q4=1; Q5=0; Q6=0; elseif (Ha==1)&& (Hb==0)&&(Hc==0) Q1=1; Q2=0; Q3=0; Q4=0; Q5=0; Q6=1; elseif (Ha==1)&& (Hb==1)&&(Hc==0) Q1=0; Q2=0; Q3=1; Q4=0; Q5=0; Q6=1; elseif (Ha==0)&& (Hb==1)&&(Hc==0) Q1=0; Q2=1; Q3=1; Q4=0; Q5=0; Q6=0; elseif (Ha==0)&& (Hb==1)&&(Hc==1) Q1=0; Q2=1; Q3=0; Q4=0; Q5=1; Q6=0; elseif (Ha==0)&& (Hb==0)&&(Hc==1) Q1=0; Q2=0; Q3=0; Q4=1; Q5=1; Q6=0; end end
Calcul des tensions à appliquer au moteur BLDC
Selon le circuit de la figure ci-dessous les tensions triphasées se calcul avec les formules suivantes :
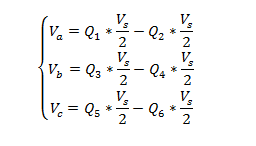
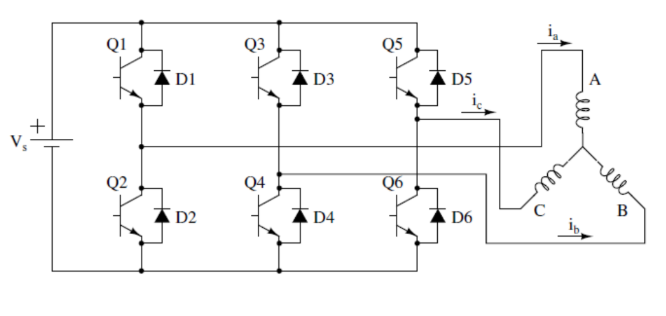
Schéma drive BLDC
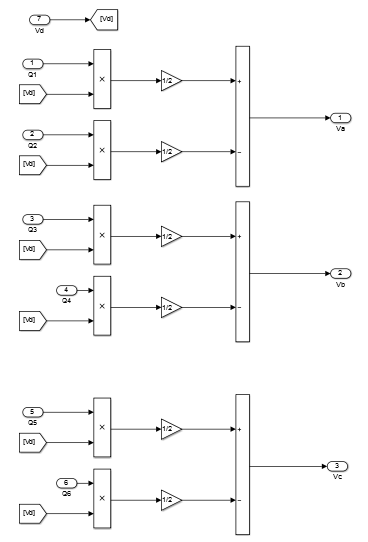


Comments
Chaffard Loïc
Super, merci, c’est un bon début pour mon projet de semestre pré-projet de Bachelor, si tous se passe bien dans mon cursus d’école d’ingénieur
matlabpourtous
Merci pour ce retour
Yamina Jouili
Merci pour tout informations,c’est un bon travail.
Bon courage
matlabpourtous
Merci pour ces encouragements
Lucas
Bonjour,
C’est super bien détaillé, mais j’ai une question concernant les expressions des forces contre-électromotrice e_a, e_b et e_c. D’où vient le divisé par 2 dans les formules ?
Par définition on dit E = ke*Omega, avec E la force électromotrice, Omega la vitesse de rotation du rotor. A cette formule vous avez ajouté la fonction Tra() que je comprend, mais je ne comprend pas pourquoi vous avez divisé le tout par 2 ?
Lucas
SAGNA
Le 2 c’est le nombre de paire de pôles de la relation angle Elec angle meca
Bouleaud Tom
Bonjour,
Pourquoi vous utiliser l’angle électrique et pas l’angle mécanique pour définir les forces contre-électromotrices ?
Sagna
C’est au choix car Il ya le nombre de paire de pôles qui les relis.
Jouili yamina
Peut vous de faire modélisation de moteur BLDC + commande trapézoïdal et merci par avant
SAGNA
Vous aurez un modèle sous peu
Rahmouni Ayoub
Merci beaucoup pour ce travail.
matlabpourtous
Merci
Rahmouni Ayoub
Bonjour, j’ai une question s’il vous plaît, pour vous avez utilisé un intégrateur discret au lieu d’un intégrateur normale (continuer) pour trouver le courant ia et ib ??
Cordialement.
sucheful
Bonjour, excellente analyse du fonctionnement du moteur BLDC. Je n’ai pas pu télécharger les fichiers d’exemple, s’il vous plaît si vous pouviez voir le lien pour les télécharger. Merci
Donald
salut a tous le cours a ete bien explique la dedans mais j aimerai avoir le fichier Simulink. j ai telecharger ca mais kand je l ouvre c est vide. et meme 0Byte
TBATIT
Merci bcp