Description
MATLAB est un système interactif et convivial de calcul numérique et de visualisation graphique destiné aux ingénieurs et scientifiques. Il possède un langage de programmation à la fois puissant et simple d’utilisation. Il permet d’exprimer les problèmes et solutions d’une façon aisée, contrairement aux autres langages de programmation. MATLAB intègre des fonctions d’analyse numérique, de calcul matriciel, de traitement de signal, de visualisation graphique 2D et 3D, etc.
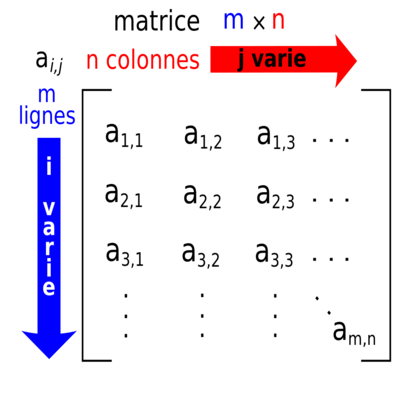
Matlab est un logiciel de calcul matriciel, maitriser la manipulation des matrices est essentiel pour la prise en main de son langage. Une matrice est un tableau rectangulaire avec m lignes et n colonnes et contenant des éléments numérique de même type.
Les fonctions mathématiques fournissent une gamme de méthodes de calcul numériques pour analyser des données, développer des algorithmes et créer des modèles. Les fonctions de base utilisent des bibliothèques optimisées pour le processeur pour les calculs vectoriels et matriciels rapides.
Objectif de la formation
L’objectif de la formation est d’apprendre les bases du puissant outil MATLAB. Cette formation offre également toutes les compétences nécessaires pour pouvoir manipuler des matrices MATLAB. Nous allons par la suite étudier les opérations arithmétiques, la trigonométrie, les fonctions statistiques, les opérations relationnelles et logiques et les polynômes dans MATLAB.
Public concerné
Etudiant, Ingénieurs, développeurs, scientifiques, enseignant, chercheurs.https://matlabpourtous.com/formation/course/les-matrices-dans-matlab/
Prérequis
Une formation initiale scientifique est souhaitable.